Mobile Money in Kenya: A Replication Exercise
Introduction
In this post I will (attempt to) replicate the main results from Mobile Money and Economic Activity: Evidence from Kenya by Fabregas and Yokossi (2022). 1 The authors study the economic effect of access to M-PESA, a service which allows users to send and receive e-money on their mobile phones via SMS. The service was introduced in 2007 in Kenya by Safaricom (a telecoms company), and it relies on a network of over 300,000 mobile money agents. Mobile money agents are typically located in local convenience stores and airtime retailers, where users can deposit cash or withdraw e-money. Prospective agents must apply for licenses with Safaricom. Fabregas and Yokossi exploit the geographic heterogeneity in M-PESA agent density (in other words, different regions received their first M-PESA agents at different times) and use a staggered difference-in-differences (DID) approach to estimate treatment effects.
From a replication perspective, this paper is also interesting because we get to work with some interesting spatial data (nightlights!) and briefly explore the Python API for the Google Earth Engine. Also, since (almost) all of the data is publicly available we should be able to replicate the paper’s results …
Data Sources
I work with 3 datasets for this replication:
Nightlights
For their outcome, Fabregas and Yokossi use nightlights as a proxy for economic activity. In particular, they use the popular DMSP-OLS datasets, which contain annual global nightlights data for 1992-2013 at the pixel level (a pixel represents an area of approximately 0.9km2). For the years in which multiple satellites collected nightlights data, the authors take the average values produced by these satellites as their outcome. DMSP-OLS data can be downloaded here, or accessed through the Google Earth Engine API.
M-PESA Agents
In 2015, FSD Kenya (in collaboration with several other organizations) collected data on the locations of around 68,000 mobile money agents across Kenya, as part of the 2015 FinAccess Geospatial Mapping Survey. Along with precise coordinates, the survey also collected information on when each agent began its operations. Using this data, Fabregas and Yokossi define a particular pixel’s “treatment year” (i.e. the year it first received access to M-PESA) based on the first year in which an M-PESA agent is less than 5km from that pixel.
Sublocations
Sublocations are the most granular administrative boundary in Kenya. As of 2009 there were 6631 sublocations in Kenya. The authors match every pixel to its corresponding sublocation, and use sublocation by year fixed effects in later analysis. Suprisingly, data on sublocations was particularly difficult to find. Fabregas and Yokossi explain that they use administrative divisions data from “the 2009 master shapefile of the Kenya National Bureau of Statistics” which “contain sublocation-level population counts and densities”, but I was unable to find these files on the KNBS website. I did, however, find a page from the World Resources Institute with a shapefile containing population density in 1999 at the sublocation-level. I’m going to proceed with the next steps using this dataset, but as we’ll soon see this may cause some issues in producing exact replications.
Data Cleaning
I’m going to complete all of the data cleaning steps in Python. Let’s begin by processing the nightlights data. There is a Python API for the Google Earth Engine (the ee library), which we’ll use to access and clean the DMSP-OLS datasets. But first let’s import all of the necessary Python libraries:
import os
import ee
import geemap
import pandas as pd
import numpy as np
from multiprocessing import Pool
import geopandas as gpd
from shapely.geometry import PointWe can initialize the Earth Engine API2 as follows:
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()Let’s extract the nightlights for the analysis period (2000-2013), collect the names of each of the unique satellite-year combinations, and import a shapefile containing the geographic boundaries for the entirety of Kenya:
collection = ee.ImageCollection("NOAA/DMSP-OLS/NIGHTTIME_LIGHTS").filterDate('2000-01-01', '2013-12-31')
# get names of all images and stores in python list (getInfo() converts from ee List to python list):
sat_names = collection.aggregate_array("system:index").getInfo()
kenya = geemap.shp_to_ee("data/sublocs_all/sublocs_all.shp")(NOTE: sublocs_all.shp was produced by merging all of the geometries in the sublocation-level shapefile. See GitHub repo for more details).
Observe that we currently have the nightlights data as an ee object (specifically as an ImageCollection). For further analysis we will need to convert everything to a pandas dataframe. Here are some user-defined functions (which are slightly modified versions from this Stack Exchange post) that allow us to convert our ee Images to dataframes:
def ee_array_to_df(arr, list_of_bands):
"""
Transforms client-side ee.Image.getRegion array to pandas.DataFrame.
Modification of
https://developers.google.com/earth-engine/tutorials/community/intro-to-python-api-guiattard
"""
df = pd.DataFrame(arr)
# Rearrange the header.
headers = df.iloc[0]
df = pd.DataFrame(df.values[1:], columns=headers)
# Remove rows without data inside.
df = df[['longitude', 'latitude', 'time', *list_of_bands]].dropna()
# Convert the data to numeric values.
for band in list_of_bands:
df[band] = pd.to_numeric(df[band], errors='coerce')
# Convert the time field into a datetime.
df['datetime'] = pd.to_datetime(df['time'], unit='ms')
# Keep the columns of interest.
df = df[['datetime', "longitude", "latitude", *list_of_bands]]
return df
def image_to_df(sat, geometry):
"""
Extract nightlights data for a particular geometry/region and satellite-year, and convert to dataframe.
"""
bands = ["stable_lights"]
collection = ee.ImageCollection(ee.Image(f"NOAA/DMSP-OLS/NIGHTTIME_LIGHTS/{sat}").select("stable_lights"))
collection_area_of_interest = collection.getRegion(geometry, scale = collection.first().projection().nominalScale()).getInfo()
df_area_of_interest = ee_array_to_df(collection_area_of_interest, bands)
return df_area_of_interestNow we iteratively apply these functions to each satellite-year to get a panel of all pixels in Kenya, from 2000 to 2013:
pixels = pd.concat(map(lambda x: image_to_df(x, kenya), sat_names), axis = 0, ignore_index=True)
print(pixels.head())| datetime | longitude | latitude | stable_lights |
|---|---|---|---|
| 2000-01-01 00:00:00 | 34.1458 | 3.82917 | 0 |
| 2000-01-01 00:00:00 | 34.1542 | 3.82917 | 0 |
| 2000-01-01 00:00:00 | 34.1625 | 3.82917 | 0 |
| 2000-01-01 00:00:00 | 34.1708 | 3.82917 | 0 |
| 2000-01-01 00:00:00 | 34.1792 | 3.82917 | 0 |
As we can see, pixels is a pandas dataframe containing pixel nightlight values (stable_lights) across years, as well as the latitude and longitude of pixel centroids. But this is not a panel yet - we should first take average nightlight values across the same pixels in the same years observed by different satellites, as the authors do:
groupvars = ["datetime", "longitude", "latitude"]
# NOTE: reset index will add grouping var row entries for ALL rows, not just for the first row in each group
pixels_avg = pixels.groupby(groupvars).agg(mean_stable =pd.NamedAgg(column="stable_lights", aggfunc=np.mean)).reset_index()
pixels_avg["year"] = pixels_avg["datetime"].dt.year # year column is just int32 typeNow we need to match these pixels to their sublocations, but we can’t do that with 2 numeric columns containing pixel latitude and longitude. Instead we’re going to convert our data to geopandas dataframes, which will have a geometry column that can be used for spatial joins. Let’s import our sublocations shapefile as a geopandas dataframe, and convert our pixels data to a geopandas dataframe too:
sublocs = gpd.read_file("data/ke_popd99lmb/ke_popd99lmb.shp")
pixels_geom = gpd.GeoDataFrame(
pixels_avg,
geometry=gpd.points_from_xy(pixels_avg.longitude, pixels_avg.latitude, crs = "EPSG:4326")
)
pixels_geom.to_crs(sublocs.crs, inplace=True)geopandas dataframe is using the same CRS (Coordinate Reference System). At a high level the CRS defines how locations in a 3 dimensional space are converted to coordinates in a 2D map. If
our 2 dataframes are using different “rules” to execute this conversion, then geopandas won’t be able to define relationships between our dataframes. To get around this, we reproject pixels_geom to use the same CRS as sublocs with the to_crs() method.Now we can conduct our spatial join:
subloc_pixels = pixels_geom.sjoin(sublocs, how = "inner", predicate="within")sjoin matches every row in pixels_geom with a row in sublocs based on the specified predicate. Here we use predicate="within", which will match any row in the left dataframe if it’s geometry is contained within the geometry of a row in the right dataframe. how = "inner" just produces an inner join in the usual sense (i.e. only rows in pixels_geom which have a matched row in sublocs are preserved).
Now all that’s left to do is merge our current dataset with the M-PESA agents data and define the appropriate “treatment year” for each pixel.
agents = pd.read_excel("data/Mobile Money Agents Database Aggregated for Distribution.xlsx")
agents[["GPS Latitude", "GPS Longitude"]] = agents[["GPS Latitude", "GPS Longitude"]].replace("--", np.nan).astype(float)
agents = agents.dropna(subset=["In What Year Did the Establishment Begin Operations"])
agents["year"] = agents["In What Year Did the Establishment Begin Operations"].apply(pd.to_datetime).dt.yearAs with our pixels dataframe, we will need to convert agents to a geopandas dataframe, using the Latitude and Longitude columns to form the geometry:
agents_geom = gpd.GeoDataFrame(
agents,
geometry=gpd.points_from_xy(agents["GPS Longitude"], agents["GPS Latitude"], crs = "EPSG:4326")
)
# Again making sure we reproject to use the same CRS across all dataframes!
agents_geom.to_crs(subloc_pixels.crs, inplace=True) To define treatment years we first need to find, for each pixel and year, the distance to the nearest agent. We can do this with a simple for-loop in combination with sjoin_nearest:
# remove index_right column produced from previous sjoin
sl_pixel_agent.drop(columns=["index_right"], inplace=True)
for y in range(2007, 2012):
agent_df = agents_geom[(agents_geom["year"] == y)].rename(columns={"year":f"year_{y}", "geometry":f"geometry_{y}"})[[f"year_{y}", f"geometry_{y}"]]
agent_df.set_geometry(f"geometry_{y}", inplace=True)
sl_pixel_agent = gpd.sjoin_nearest(sl_pixel_agent, agent_df, how = "left", max_distance = 5000, distance_col = f"dist_{y}").set_geometry("geometry")
print(f"YEAR == {y}, length of sl_pixel_agent is {len(sl_pixel_agent)}")
sl_pixel_agent.drop(columns=["index_right"], inplace=True)
sl_pixel_agent.drop_duplicates(inplace=True)
# duplicates appearing because a single pixel is equidistant to multiple agents. sjoin_nearest works like sjoin, except matches occur based on which row in the right dataframe (agent_df) is closest to a given row in the left dataframe (sl_pixel_agent), rather than according to some predicate. We save the distance to the closest agent for each year in dist_{y} columns for each y in the interval $[2007, 2011]$.
For each pixel, we can use a mask to select the first year in which a mobile money agent is less than 5km away from its centroid. The authors define this year as year 0, and a pixel is defined as being “treated” (i.e. having access to mobile money) for every year after year 0. Each pixel’s year 1 (the first year of treatment) is referred to as the wave of treatment.
# collect the columns dist_2007, dist_2008 ...
year_columns = [col for col in sl_pixel_agent.columns if col.startswith('dist_')]
# Create a boolean mask for distances < 5000
mask = (sl_pixel_agent[year_columns] < 5000).astype(int)
# find first column (from left to right) which has mask == 1 for each row
first_valid_years = mask.idxmax(axis=1)
first_valid_years[mask.sum(axis=1) == 0] = np.nan # if a pixel has no year with distance < 5000, then assign NA
# Extract year from the column names
sl_pixel_agent['year0'] = first_valid_years.str.extract(r'(\d{4})').astype(float)
sl_pixel_agent["wave"] = sl_pixel_agent["year0"] + 1Ok, nearly there! The last thing to do is filter the data to obtain what the authors describe as the “analysis sample”. First we exclude “areas with densities below 4 ppl/km2 in 1999” (I interpret “areas” to mean “sublocations” since we don’t have population density data at a lower level of aggregation). We also exclude pixels that had not “gained access to a mobile money agent during the first five waves of the M-PESA rollout”. Finally, we drop “[s]ublocations that have no pixel ever lit during the study period (2000–2013).”
analysis = sl_pixel_agent[(sl_pixel_agent["GRTOT_DENS"] >= 4) & (sl_pixel_agent["year0"].between(2007, 2011))]
subloc_filter = analysis.groupby("SLID")["mean_stable"].transform(lambda x: not all(x==0))
analysis = analysis[subloc_filter]Time to export and move to R for some regressions:
# to_file will complain if we don't convert datetime columns to strings
analysis["datetime"] = analysis["datetime"].astype(str)
analysis.to_file("data/analysis.shp")Analysis
For their main specification, Fabregas and Yokossi use a staggered DID regression of the following form:
$$ \begin{align*} \text{std.L}_{it} = \alpha_{i} + \gamma_{t} + \sum_{t} \beta_{t} \text{Access}_{it} + \theta \mathbf{X}_{it} + \delta_{i}t + \epsilon_{it} \end{align*} $$ where:
- $\text{std.L}_{it}$ is a standardized measure of nightlights for pixel $i$ in year $t$
- $\alpha_{i}$ and $\gamma_{t}$ are pixel and year fixed effects respectively
- $\text{Access}_{it}$ “indicates a set of dummy variables that take the value 1 if a cell had received M-PESA access in year t, for years following year 0” (i.e. the relative time indicators for the post-treatment periods)
- $\mathbf{X}_{it}$ are time-varying controls. The authors run multiple specifications using different $\mathbf{X}_{it}$
- $\delta_{i}t$ are pixel-level linear time trends
Standard errors are clustered at the district level.
As a test for parallel pre-trends, the authors also run the following specification:
$$ \begin{align*} \text{std.L}_{it} = \alpha_{i} + \gamma_{t} + \sum_{t} \beta_{t} \text{Relative Access}_{it} + \theta \mathbf{X}_{it} + \epsilon_{it} \end{align*} $$
where $\text{Relative Access}_{it}$ include relative time indicators for all periods in $[-6, 6]$ except period $0$. In other words, we now include relative time indicators for lead years (as well as the lag years as before). The authors only run one version of this event study regression, where $\mathbf{X}_{it}$ just contains 1 additional control (sublocation by year fixed effects).
Let’s load the R packages we’re going to use:
# remove existing objects from environment
rm(list = ls())
# list of required packages
req_packages <- c("tidyverse", "stargazer", "devtools", "haven", "sandwich",
"readxl", "terra", "sf", "geodata", "lfe", "fixest", "broom",
"gridExtra", "future.apply", "purrr", "grid", "lmtest", "patchwork",
"ggthemes", "modelsummary", "tinytable", "tinytex", "webshot2",
"gt", "flextable", "ftExtra", "gdtools", "officer", "rlang", "showtext",
"extrafont", "latex2exp", "knitr")
# function to install required packages
install_req <- function() {
reqs <- req_packages[!req_packages %in% installed.packages()]
if (length(reqs) > 0) {
install.packages(reqs)
} else {
message("Nothing to install")
}
}
# function call
install_req()
# Load requirements
invisible(lapply(req_packages, require, character.only = TRUE))To replicate the main results, we first need to construct the relative time indicators and standardize our nightlights outcome. We can load in the analysis dataset we produced in python and create the required variables in a copy:
analysis <- st_read("data/analysis.shp")
analysis2 <- analysis %>%
mutate(sdlight = (mean_stabl - mean(mean_stabl)) / sd(mean_stabl),
rel_year = year - year0,
pixel = paste(latitude, longitude, sep = ", ")) %>%
gen_rel(var = "rel_year", reltimes = -6:6) %>%
group_by(pixel) %>%
arrange(pixel, year) %>%
mutate(avg_pre_def = (mean(mean_stabl[year == 2006]) - mean(mean_stabl[year == 2000]))/mean(mean_stabl[year == 2000])) %>%
mutate(avg_pre = case_when(mean_stabl[year == 2000] == mean_stabl[year == 2006] ~ 0,
.default = mean(avg_pre_def) )) %>%
ungroup()sdlight will be our outcome measure for the regressions, while rel_year provides us with the relative time of each observation. We create pixel for pixel fixed effects. The variable avg_pre is the pixel-level growth rate in nightlights from 2000 to 2006, and is used as a control in one of the specifications (note that we separately deal with the case where nightlights in 2000 are equal to 2006, because if nightlights in 2000 equals 0 we get a 0 / 0 error, and R will produce NAs).
gen_rel is a function I create to generate relative time indicators:
gen_rel <- function(df, var, reltimes) {
for (y in reltimes) {
if (y < 0) {
name = paste0("dm", gsub("-", "", y))
} else {
name = paste0("d", y)
}
df <- df %>% mutate(!!name := as.integer(!!sym(var) == y))
}
return(df)
}This function will generate relative time dummies using an arbitrary var (which in our case is rel_year). Note that the sym function from rlang allows us to reference the variable as a string and convert it to a symbol, which can then be used for variable assignment with tidyverse functions.3 Here we label negative time dummies with the prefix “dm”, and other dummies with “d”.
Time to run the regressions! We’ll use feols from the fixest package to implement the following 5 variations of the main specification:
- Pixel and year FEs, no other controls.
- Pixel, year, and sublocation by year FEs.
- Pixel, year, sublocation by year, and growth rate in 2000-2006 by year FEs (i.e.
avg_prebyyear). - Pixel, year, and sublocation by year FEs, as well as pixel-level linear trends.
- Specification 4. but excluding pixels that were treated in the first wave (i.e.
year0 == 2007)
# TWFE
lm_main1 <- feols(fml = sdlight ~ d1 + d2 + d3 + d4 + d5 + d6 | pixel + year,
data = analysis2,
cluster = ~DISTID)
# add sublocation (SLID) by year FEs
lm_main2 <- feols(fml = sdlight ~ d1 + d2 + d3 + d4 + d5 + d6 | pixel + year + SLID^year,
data = analysis2,
cluster = ~DISTID)
# add pre-period growth rate (avg_pre) by year FEs
lm_main3 <- feols(fml = sdlight ~ d1 + d2 + d3 + d4 + d5 + d6 | pixel + year + SLID^year + avg_pre^year,
data = analysis2,
cluster = ~DISTID)
# add unit specific linear time trends
lm_main4 <- feols(fml = sdlight ~ d1 + d2 + d3 + d4 + d5 + d6 | pixel[year] + year + SLID^year,
data = analysis2,
cluster = ~DISTID)
# drop wave 1 and estimate equation 4
lm_main5 <- feols(fml = sdlight ~ d1 + d2 + d3 + d4 + d5 | pixel[year] + year + SLID^year,
data = analysis2 %>% filter(year0 != 2007),
cluster = ~DISTID)Using these models we can reproduce Table 3 (the main results table) from Fabregas and Yokossi (2022) as follows:
(Note that the code for formatting the table using modelsummary and flextable is included below, but for the sake of brevity I won’t go into the details. I’ll write up a separate post that walks through these packages …')
click to reveal table replication code
lm_all <- list(
"(1)" = lm_main1,
"(2)" = lm_main2,
"(3)" = lm_main3,
"(4)" = lm_main4,
"(5)" = lm_main5
)
# function to get reformatted independent var names in table
rename_year <- function(old) {
new <- paste0("Year " , as.integer(gsub("[^0-9]", "", old)))
setNames(new, old)
}
# from https://stackoverflow.com/questions/77886224/how-to-format-observation-numbers-with-commas-in-modelsummary-output-in-r
format_nobs <- function(x) {
if (is.numeric(x)) {
return(format(x, big.mark = ",", scientific = FALSE))
}
return(x)
}
modelsummary(lm_all,
output = "flextable",
fmt = 3,
coef_omit = "Intercept",
stars = c("*" = .1, "**" = .05, "***" = .01),
coef_rename = rename_year,
gof_map = list(list("raw" = "nobs", "clean" = "Observations", "fmt" = format_nobs))) -> tbl3
register_gfont("Merriweather")
register_gfont("IBM Plex Sans")
tbl3 %>%
add_header_row(values = c("", "Analysis sample", "Excluding wave 1"), colwidths = c(1, 4, 1)) %>%
add_header_row(values = c("", ""),
colwidths = c(1, 5)) %>%
compose(i = 1, j = 1, part = "header", value = as_paragraph(as_b("Table 3."), " Main Results")) %>%
bg(bg = "transparent", part = "all") %>%
align(j=2:6, align = "center", part = "all") %>%
font(fontname = "Merriweather", part = "all") %>%
font(i = 1, fontname = "IBM Plex Sans", part = "header") %>%
set_table_properties(width = 1) %>%
bold(i = 2:3, part = "header") %>%
border_remove() %>%
autofit() -> tblflex
# black-on-white image
tblflex %>%
border(part = "header", border.bottom = fp_border_default(color = "#000000")) %>%
border(part = "footer", border.top = fp_border_default(color = "#000000")) %>%
save_as_image("output/lm_all_test.png", webshot = "webshot", res = 400)
# white-on-black image
tblflex %>%
border(part = "header", border.bottom = fp_border_default(color = "#FFFFFF")) %>%
# for some reason color is not rendering correctly when we set top footer for footer
# (rather than bottom footer for last row)
border(part = "body", i = 13, border.bottom = fp_border_default(color = "#FFFFFF")) %>%
color(color = "#FFFFFF", part = "all") %>%
save_as_image("output/lm_all_test_dark.png", webshot = "webshot", res = 400)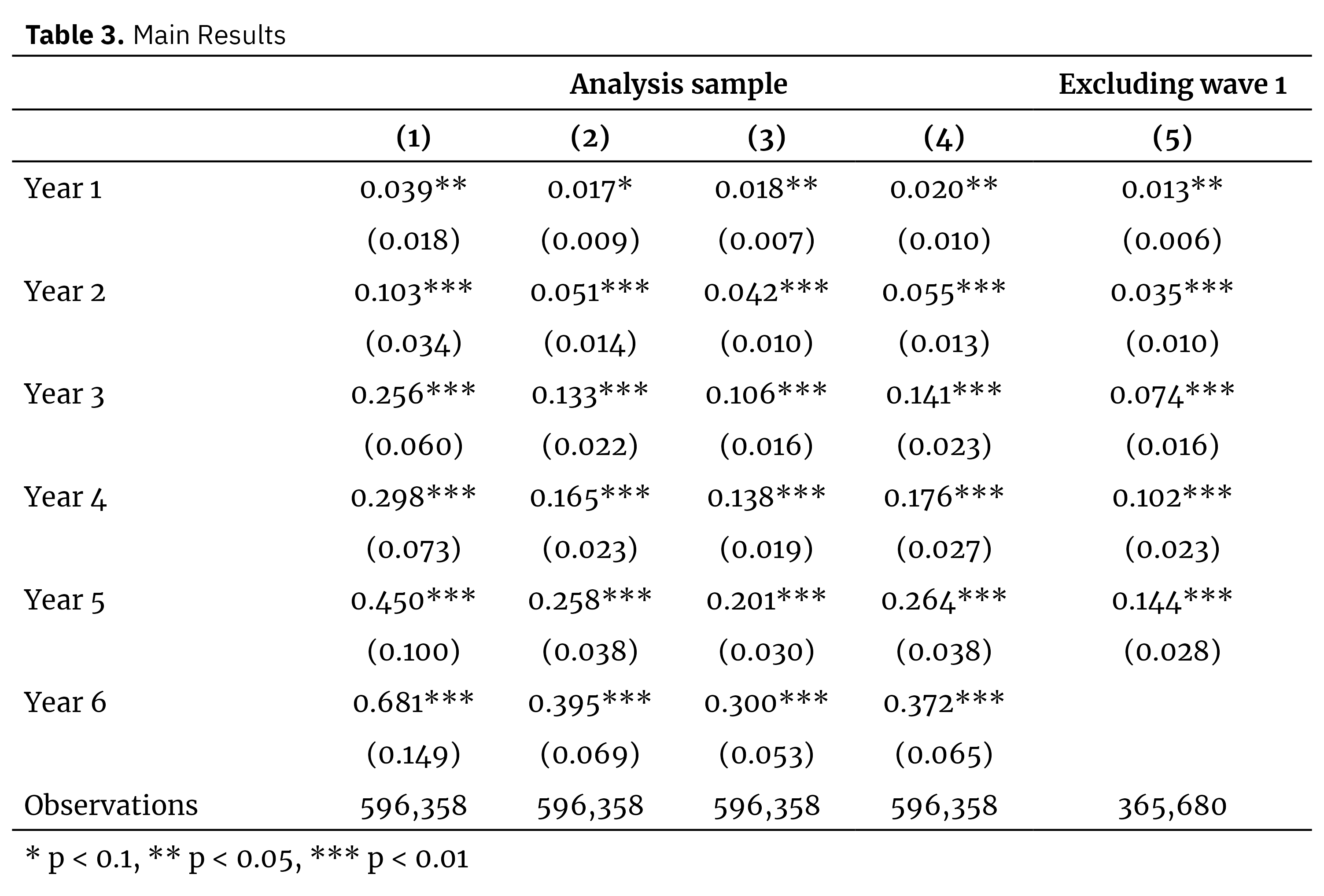
Replication of Table 3 from Fabregas and Yokossi (2022)
Now, on to the event study. The regression itself is a straightforward extension of the main specification (i.e. just including the negative relative time indicators):
# looking at pre-trends
lm_event <- feols(fml = sdlight ~ dm6 + dm5 + dm4 + dm3 + dm2 + dm1 +
d1 + d2 + d3 + d4 + d5 + d6 | pixel + year + SLID^year,
data = analysis2,
cluster = ~DISTID)We can extract the coefficients of interest with coeftest, and then clean up the variable names and include confidence intervals with some of the tidyverse tools:
# create dataframe of coefficients
coeftest(lm_event) %>%
tidy %>%
filter(str_detect(term, "^dm.*\\d$") | str_detect(term, "^d.*\\d$")) %>%
mutate(year = str_replace(term, "^dm", "-")) %>%
mutate(year = str_replace(year, "^d", "")) %>%
mutate(year = as.numeric(year)) %>%
mutate(lb = estimate - qnorm(0.95) * std.error,
ub = estimate + qnorm(0.95) * std.error) %>%
add_row(term = "d0", estimate = 0, std.error = 0, statistic = 0, p.value = 0,
year = 0, lb = 0, ub = 0, .after = 6) -> dfevent
view(dfevent)| term | estimate | std.error | statistic | p.value | year | lb | ub |
|---|---|---|---|---|---|---|---|
| dm6 | 0.0050906 | 0.0021202 | 2.4010128 | 0.0163501 | -6 | 0.0016032 | 0.0085781 |
| dm5 | 0.0060683 | 0.0029029 | 2.0904129 | 0.0365812 | -5 | 0.0012934 | 0.0108432 |
| dm4 | -0.0092225 | 0.0041774 | -2.2077101 | 0.0272649 | -4 | -0.0160937 | -0.0023513 |
| dm3 | 0.0006112 | 0.0048771 | 0.1253202 | 0.9002701 | -3 | -0.0074109 | 0.0086333 |
| dm2 | -0.0027173 | 0.0040949 | -0.6635780 | 0.5069607 | -2 | -0.0094528 | 0.0040182 |
| dm1 | 0.0019423 | 0.0041625 | 0.4666090 | 0.6407799 | -1 | -0.0049044 | 0.0087889 |
| d0 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0 | 0.0000000 | 0.0000000 |
| d1 | 0.0176687 | 0.0080894 | 2.1841765 | 0.0289497 | 1 | 0.0043628 | 0.0309746 |
| d2 | 0.0514006 | 0.0134282 | 3.8278001 | 0.0001293 | 2 | 0.0293131 | 0.0734881 |
| d3 | 0.1330742 | 0.0214348 | 6.2083274 | 0.0000000 | 3 | 0.0978171 | 0.1683313 |
| d4 | 0.1652521 | 0.0223511 | 7.3934539 | 0.0000000 | 4 | 0.1284878 | 0.2020165 |
| d5 | 0.2581600 | 0.0377355 | 6.8413075 | 0.0000000 | 5 | 0.1960907 | 0.3202294 |
| d6 | 0.3951391 | 0.0683204 | 5.7836174 | 0.0000000 | 6 | 0.2827620 | 0.5075161 |
Here’s the ggplot code to format the figure as in the paper:
click to reveal figure replication code
# load Google fonts for use in ggplot
loadfonts(device = "win")
font_add_google("Merriweather")
font_add_google("IBM Plex Sans")
showtext_auto()
# produce coefficient plots
ggplot(data = dfevent,
aes(x = year, y = estimate, ymin = lb, ymax = ub)) +
geom_point(shape = 18, size = 0) +
geom_errorbar(width = 0.15, color = "#A9A9A9", linewidth = 0.75) +
scale_x_continuous(breaks = seq(-6, 6),
labels = c(as.character(seq(-6, 6)) )) +
scale_y_continuous(breaks = c(0, 0.2, 0.4, 0.6), limits = c(-0.1, 0.6)) +
labs(x = "Year", y = "Lights",
title = latex2exp::TeX("\\textbf{Figure 4. } Event Study")) +
theme_stata(scheme = "s1mono") +
theme(plot.title = element_text(family = "IBM Plex Sans", hjust = 0, size = 8),
axis.text = element_text(size = 8, family = "Merriweather"),
axis.title.x = element_text(size = 10, family = "Merriweather"),
axis.title.y = element_text(size = 10, margin = margin(r=5), family = "Merriweather"),
panel.grid.major.y = element_blank(),
panel.background = element_rect(fill='transparent'),
plot.background = element_rect(fill='transparent', color=NA)) -> event
event +
geom_path(linetype="dashed") +
geom_hline(aes(yintercept = 0), linetype = "dashed") +
geom_vline(aes(xintercept = 0), linetype = "dashed") -> event_light
ggsave("output/event_study.svg", plot = event_light, bg = "transparent")
# dark mode version:
event +
geom_path(linetype="dashed", color = "#ffffff") +
geom_hline(aes(yintercept = 0), linetype = "dashed", color = "#ffffff") +
geom_vline(aes(xintercept = 0), linetype = "dashed", color = "#ffffff") +
theme(panel.background = element_rect(fill='transparent', color = "#ffffff"),
axis.line.x.bottom=element_line(color="#ffffff"),
axis.line.y.left = element_line(color="#ffffff"),
axis.ticks.x = element_line(color = "#ffffff"),
axis.ticks.y = element_line(color = "#ffffff"),
axis.title = element_text(color = "#ffffff"),
axis.text.x = element_text(color = "#ffffff"),
axis.text.y = element_text(color = "#ffffff"),
plot.title = element_text(color = "#ffffff")) -> event_dark
ggsave("output/event_study_dark.svg", plot = event_dark, bg = "transparent")
Replication of Figure 4 from Fabregas and Yokossi (2022)
Evaluation
Beginning with Table 3, we can clearly see that the results have not been replicated exactly. Our results are generally slightly smaller than those of the paper, except for a couple of the coefficients for specification (5). However, our results certainly tell the same story, namely that the coefficients for the early relative time indicators are small but significant, and noticeably increase in size for the later years. The same is true for the event study. It is difficult to make a quantitative comparison here since Fabregas and Yokossi do not provide the exact coefficient sizes for the event study regression. However a visual inspection suggests that our results are very close to those of the paper in terms of magnitude (although the confidence intervals for later years are fairly different).
There are a number of possible reasons for the results not aligning exactly. My primary suspicion is that we are using different shapefiles for the sublocations, and so we end up with a different analysis sample. Indeed, our sample is just 42,597 pixels while the paper is working with 44,105 pixels, and these “missing pixels” might be due to missing sublocations in our 1999 shapefile. The authors use the “2009 master shapefile” from KNBS for sublocation data, and according to the paper “[u]ntil the 2009 national census, the country was divided into … 6631 sublocations”, while the data I’m using only contains 6622 sublocations.
My plan is to search again for the “master shapefile” of sublocations – if I find anything it will probably feature in a future writeup …
Raissa Fabregas, Tite Yokossi, Mobile Money and Economic Activity: Evidence from Kenya, The World Bank Economic Review, Volume 36, Issue 3, August 2022, Pages 734–756, https://doi.org/10.1093/wber/lhac007 ↩︎
Note that to run my code you will need to set up Earth Engine using your own Google account here ↩︎
